康德书信《致奥古斯特·威廉·雷贝格》1790年9月25日之前

54　致奥古斯特·威廉·雷贝格

1790年9月25日之前

题目是，为什么任意创造数字的知性不能思维数字中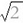？因为，如果知性思这个数字，那么，它就必须像表现的那样也制造这个数字。数字是知性自主性的纯粹运用，算术和代数的综合命题，都不能通过空间和时间中的直观条件限制这种运用。看来，必须假设一种想象力的先验能力，这种能力在客体的表象中，甚至不依赖空间和时间，仅仅依据知性把表象综合地联结起来，并从知性中引申出一个代数学的特殊体系，对这个体系的进一步认识，把解方程式的方法提高到最大的普遍性。

我就是这样理解向我提出的这个问题的。

试回答这个问题如下：

1.我可以把任何数字看作两个因数的乘积，即使这两个因数并没有给予我，而且从来不能在数字中被给予。因为，如果已知的数字是15，那么，我就可以设定，这个数字由以产生的一个因数是3，而另一个因数就是5，结果是3×5=15。或者已知的因数是2，则找到的另一个因数就是15/2。或者第一个因数是一个分数1/7，则另一个因数就是105/7，等等。因此，如果已知一个因数，为任何一个作为乘积的数字找到另一个因数是可能的。

2.但是，如果不知道两个因数中的任何一个，只有两个因数的比例是已知的，例如两个因数相等，已知数是a，所找到的因数是x，那么，比例式就是1：x=x：a，也就是说，x是1与a之间的中间几何等比数。由于a=x2与此相符合，所以，x=，即一个已知量的平方根，例，是通过1与已知数2之间的中间等比数来表述的。思维这样一个数字也是可能的。

正方形的对角线表明，我们能够在一个数字1和另一个数字2之间找到一个中间等比量。因此，问题在于，为什么不能为这个限量找到一个数字，使它可以在概念中清楚地、完全地表现这个限量的量[它与单一（Einheit）的关系]。

任何一个数字作为平方都必然可以由另一个作为平方根的数字来表现。但从这里并不能得出结论，认为这个作为平方根的数字必然是有理数，即必然与单一之间有一种可数的关系。按照同一性的原理，即从两个相等的（但不确定的）因数得出一个已知的乘积，这一点是可以看出来的。因为在这两个因数中，它们与单一之间的关系根本不是已知的，只有它们相互之间的关系才是已知的。但是，尽管如此，在数列中，在这个数列（例如，这个数列是按十进制划分的）的两个项之间，这个平方根永远是一个中间项，在这个中间项中，可以找到它与单一之间的关系。这个结论是从上述第一点得出的，即如果在这个数列中找到一个平方根的项的话。但是，任意制造这个概念的知性，却不能创造这个完善的数字概念，不得不满足于在这种规定中选取对数字的无穷接近。这在实际上是以作为一切计数和数量的形式的渐进为基础的，因而是以作为这种数量产生基础的条件为基础的。

尽管一个正量的平方的单纯概念，按照它在代数中的表现方式，根本不需要在时间中的综合，同样，对一个负量的平方根的不可能性的认识，也不需要这种综合（在这个负量的平方根中，作为正量的单一和另一个量x的关系，必须与它和一个负量x的关系相同由于这是矛盾的，所以是一个不可能的量的表述。），不用触动时间条件，这种不可能性就可以从单纯量的概念中认识到。但是，一旦已知的不是a，而是a所表示的数字，为了不仅像在代数中那样标示出这个数字的平方根，而且要像在算术中那样找到它的平方根，一切数字产生的条件，即时间，就不可避免地成为基础。时间作为纯直观，我们不仅可以在其中认识到已知的数量，而且还可以从平方根中得到教益，无论平方根是作为整数，还是当它不可能是整数时，只是作为无理数，通过分数的无穷递减级数被找到。

并非一个数字的单纯知性概念，而是在作为一种纯直观的时间中的综合，必然构成了一个确定数字，例如15这个数字的平方根概念的基础，这由以下事实得到说明，即仅仅从一个数字的单纯概念中，我们从来不能判定，这个数字的平方根是有理的，还是无理的。我们必须就这个数字进行试验，或者是在100以内的数字中，仅仅依照乘法表，把较小整数的自乘积与已知的平方进行比较，或者按照普遍证明了的原理，在较大的数字中，通过分解这些数字，分解一个平方、一个两部分的或者多部分的平方根，从而逐渐地寻找这些数字的部分。但是，在所有那些对一个自乘的整数的试验不能得出平方的情况中，单一的除数就按照某种比例，比如十进制比例增长，这些除数也就被当作一个分数的无穷递减级数的分母。因为这个级数虽然可以任意地接近完成，但却永远不能完成，所以，这个级数就是平方根的表述（但只是以无理的方式表述）。

假设有一种我们既不能先天地证明、也不能说明它如何形成的情况，即如果一个已知量的平方根不能在整数中被找到，也不能在分数中被规定（但是尽管如此，它可以尽可能地接近这个分数），那么，这就是我们的想象力与知性关系的一种现象。我们虽然可以通过对数字进行的试验感知这种现象。但却根本不能从知性概念中解释这种现象。但是，虽然前一种情况可能会发生，推测后一种情况却是不必要的。

想象力并不适宜通过算术解释一个中间等比量的知性概念。我觉得，这个习题的作者在这方面所发现的令人惊异的东西，本来是以那些不能完全在数字中被思维的量的几何作图可能性为基础的。

因为我觉得，认为必须为每一个数字找到一个平方根，这个平方根也许本身不是数字，仅仅是依照人们的要求接近一个数字的规则，这并不应该引起知性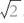感到诧异。知性应该诧异的是，这个概念可以作成几何图形，因而不仅是可思维的，而且还是可以相应地在直观中加以说明的。对此，知性根本没有认识到任何根据，甚至连假定一个客的可能性的资格也没有，因为它根本不能在数字的直观中相应地阐述这样一个量的概念，因而也就更不应该期待，这样一个限量能够先天地被给予。

在我们的直观对象的规定性中，把空间和时间这两种感性形式联结起来的必要性，即如果主体把自身当作他的表象客体，时间就必须被表象为一条直线，以便把它看作限量，反过来说，一条直线只是由于它必须在时间中被绘制，才能被看作限量，我觉得，在我们的规定存在的时间规定性中，对必须把内感觉与外感觉联结起来的认识，为证明外部事物的表象的客观实在性（又是心理学的唯心主义）提供了指南。不过，我现在不能继续研究这个问题了。